报告题目(Title): Higher Symplectic Stacks in Differential Geometry
报 告 人(Speaker):朱晨畅 德国哥廷根大学
报告地点(Location): Zoom ID:889 1241 3953,密码:330378
会议链接:https://us06web.zoom.us/j/88912413953?pwd=MXFjbkVJRzVFQ1R0WnpMSXQwZzcvZz09
Abstract: In this series of lectures, we'd like to explore higher symplectic stacks in differential geometry with the framework of Lie n-groupoids. We'll talk, in more or less details on,
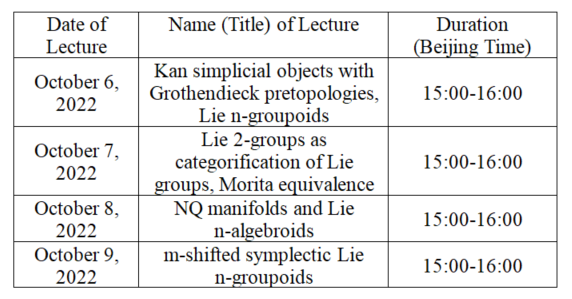
1. Kan simplicial objects with Grothendieck pretopologies, Lie n-groupoids;
2. Lie 2-groups as categorification of Lie groups, Morita equivalence: via a) hypercovers, b) weak equivalences, c) bibundles (sometimes called Hilsum-Skandalis bibundles);
3.NQ manifolds (a sort of d.g. manifolds), Lie n-algebroids (as tangent complex of Lie n-groupoids);
4. m-shifted symplectic Lie n-groupoids, with example of BG (or Lie group) together with several interesting models of symplectic forms, symplectic Morita equivalence, I.M. (infinitesimal multiplicative) forms on Lie n-algebroids, which provide models of symplectic forms.
I. Lecture Information
报告人简介:朱晨畅,德国哥廷根大学终身教授,奥林匹克数学竞赛金牌(满分)得主。1999年在北京大学获得学士学位,2004年在加州大学伯克利分校获得博士学位,瑞士苏黎世联邦理工学院博士后,2013年在德国哥廷根大学获得终身职位。从事Poisson几何,李群胚等高阶微分几何的研究。在Duke Math. J., Compos. Math., Adv. Math., JEMS, Math. Ann., Trans. Amer. Math. Soc., Comm. Math. Phys., IMRN, Ann. Inst. Fourier (Grenoble), 等杂志上发表高水平论文30余篇。